Дисконтирование денежных потоков при оценке эффективности инвестиционных проектов

Понятие и содержание значения NPV

Прежде чем при переходе к теме NPV говорить, что это такое и как его рассчитать, надо понять значение фразы, из которой складывается аббревиатура. Для словосочетания «Net present value» в отечественной экономической и математической литературе можно найти несколько традиционных вариантов перевода:

1. В первом варианте, характерном для математических учебников, NPV определяется как чистый дисконтированный доход (ЧДД).
2. Второй вариант – чистая приведённая стоимость (ЧПС) – наряду с первым считается самым употребляемым.
3. Третий вариант – чистый приведенный доход – совмещает в себе элементы первого и второго переводов.
4. Четвёртый вариант перевода термина NPV, где PV – это «текущая стоимость», наименее распространён и широкого хождения не имеет.

Независимо от перевода, значение NPV остаётся неизменным, а термин этот означает, что

NPV – это такое чистое приведённое к текущему моменту значение стоимости. То есть, дисконтирование денежного потока как раз и рассматривается как процесс установления его (потока) стоимости посредством приведения стоимости совокупных выплат к определённому (текущему) моменту времени. Поэтому определение значения чистого дисконтированного дохода (NPV) становится, наряду с IRR, ещё одним способом оценить эффективность инвестиционных проектов заранее.

На уровне общего алгоритма, чтобы определит перспективность бизнес-проекта по данному показателю, нужно сделать следующие шаги:

• оценить движение денежных потоков – первоначальные вложения и ожидаемые поступления,
• установить стоимость капитала – посчитать ставку,
• дисконтировать входящие и выходящие денежные потоки по установленному показателю ставки,
• суммировать все дисконтированные потоки, что и даст величину NPV.

Если NPV-расчет демонстрирует величины больше нуля, значит, инвестиции прибыльны. Причём, чем больше число NPV, тем больше, при прочих равных, ожидаемое значение прибыли. Учитывая, что доход кредиторов обычно бывает фиксированным, всё, что проект принесет сверх него, принадлежит акционерам – с положительным NPV акционеры заработают. Обратная ситуация с NPV меньше нуля сулит инвесторам убытки.

Возможна ситуация, при которой чистый дисконтированный доход будет равен нулю. Это означает, что денежных потоков хватает на возмещение инвестированного капитала без прибыли. При одобрении проекта с NPV равным нулю, размер компания увеличится, но цена акций останется неизменной. Но инвестирование в такие проекты может быть связано с социальными или экологическими задачами инициаторов процесса, что делает возможным инвестирование в подобные проекты.

Простые проценты

Сущность метода начисления по простым процентам состоит в том, что проценты начисляются в течение всего срока инвестиции на одну и ту же сумму (проценты начисленные за предыдущие периоды, не капитализируются, т.е. на них проценты в последующих периодах не начисляются).

В MS EXCEL для обозначения Приведенной стоимости используется аббревиатура ПС (ПС фигурирует как аргумент в многочисленных финансовых функциях MS EXCEL).

Примечание . В MS EXCEL нет отдельной функции для расчета Приведенной стоимости по методу Простых процентов. Функция ПС() используется для расчета в случае сложных процентов и аннуитета. Хотя, указав в качестве аргумента Кпер значение 1, а в качестве ставки указать i*n, то можно заставить ПС() рассчитать Приведенную стоимость и по методу простых процентов (см. файл примера ).

Для определения Приведенной стоимости при начислении простых процентов воспользуемся формулой для расчета Будущей стоимости (FV): FV = PV * (1+i*n) где PV – Приведенная стоимость (сумма, которая инвестируется в настоящий момент и на которую начисляется процент); i – процентная ставка за период начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц); n – количество периодов времени, в течение которых начисляются проценты.

Из этой формулы получим, что:

PV = FV / (1+i*n)

Таким образом, процедура расчета Приведенной стоимости противоположна вычислению Будущей стоимости. Иными словами, с ее помощью мы можем выяснить, какую сумму нам необходимо вложить сегодня для того, чтобы получить определенную сумму в будущем. Например, мы хотим знать, на какую сумму нам сегодня нужно открыть вклад, чтобы накопить через 3 года сумму 100 000р. Пусть в банке действует ставка по вкладам 15% годовых, а процент начисляется только основную сумму вклада (простые проценты). Для того чтобы найти ответ на этот вопрос, нам необходимо рассчитать Приведенную стоимость этой будущей суммы по формуле PV = FV / (1+i*n) = 100000 / (1+0,15*3) = 68 965,52р. Мы получили, что сегодняшняя (текущая, настоящая) сумма 68 965,52р. эквивалентна сумме через 3 года в размере 100 000,00р. (при действующей ставке 15% и начислении по методу простых процентов).

Конечно, метод Приведенной стоимости не учитывает инфляции, рисков банкротства банка и пр. Этот метод эффективно работает для сравнения сумм «при прочих равных условиях». Например, что с помощью него можно ответить на вопрос «Какое предложение банка выгоднее принять, чтобы получить через 3 года максимальную сумму: открыть вклад с простыми процентами по ставке 15% или со сложными процентами с ежемесячной капитализацией по ставке 12% годовых»? Чтобы ответить на этот вопрос рассмотрим расчет Приведенной стоимости при начислении сложных процентов.

About this NPV Calculator

Calculating NPV can be a very daunting task, specially when you have so many positive and negative cash flows. There’s many tool available that can be used to calculate NPV. You can either use financial calculators like Ti-83,Ti-84 and HP 12c calculator or can take the help from softwares like MS Excel. This website, npvcalculator.info is such tool. It’s an online NPV calculator.

To calculate NPV or Net Present Value, enter the initial investment, the expected discount rate and cash flows for each period. You can also add or delete period fields as needed. Then hit the calculate button to get the NPV result.

Our Other Financial Calculators:

• IRR Calculator : To calculate the internal rate of return

Как рассчитать NPV в Excel

Приведем пример расчета показателя чистой приведенной стоимости NPV в Excel, используя следующие исходные данные:

• стоимость проекта – 3 750 000 руб. (50 000 $ или 1 450 000 грн.);
• прогнозируемые поступления денежных средств: за первый год – 375 000 руб. (5 000 $ или 145 000 грн.), далее планируется прирост на 30%;
• расходы – 41 250 руб. (550 $ или 15 950 грн.) в первый год, далее увеличиваем их на 5% ежегодно.

Сначала мы посчитаем ставку дисконтирования, используя формулу Фишера. В качестве номинальной ставки возьмем ключевую ставку Центробанка, равную 4,25%. Инфляция составляет 4%.

​\( (1+r)=(1+4,25)+(1+4); \)​

​\( r=9,25 \%. \)​

Мы использовали функцию ЧПС, встроенную в Excel. Если менять значение r, можно определить, что при увеличении ставки дисконтирования NPV проекта снижается. Таким образом, многое зависит от правильности вычисления этого показателя.

Финансовые показатели бизнес-плана

Период статьи	20__ г.
Рентабельность деятельности Р з = ЧП / И
Рентабельность оборота Ро = Пп. / В х 100 %
Рентабельность продаж Рпр = П / V х 100 %
Порог рентабельности ПР. = З пост. / ((ВР – З пер.) / ВР)
Точка безубыточности Тб = З пост. / Ц ед. – З пер.
Уровень эффективности предприятия Э = Р / З
Запас финансовой прочности предприятия З фп = ВР – ПР.
Валовой доход предприятия ВД = Т х РН, РН = ТН/ (100% +ТН)

8.1. Запас финансовой прочности

Запас финансовой прочности предприятия – это разница между достигнутой фактической выручкой от реализации и порогом рентабельности.

Это определяется по формуле:

ЗФП=ВР-ПР,

где ЗФП – запас финансовой прочности,

ВР – выручка от реализации,

ПР – порог рентабельности.

Ресурс финансовой устойчивости или предела безопасности показывает, насколько вы можете сократить производство, не неся убытков.

Чем выше показатель финансовой устойчивости, тем ниже риск убытков для предприятия.

формула

Чистая приведенная стоимость: NPV = FC_N/ (1 + D)NСтавка дисконтирования: D = I/FV = (FV-PV)/FVСрок окупаемости: PBP = И/(Дп + Ам)Дисконтированный срок окупаемости: DPBP = Т t1 CFt x (1 + r) t > CF Внутренняя норма доходности: IRR = r₁ + NPV₁ / (NPV₁ — NPV₂) х (r ₂ — r ₁)

8.2. Метод чистой приведенной стоимости — NPV

NPV, или чистый дисконтированный доход — сумма расчетного потока платежей, приведенная к текущей (на настоящий момент времени) стоимости. Приведение к текущей стоимости приводится по заданной ставке дисконтирования.

Этот метод учитывает взаимосвязь между денежными потоками и временем. Если рассчитанная чистая стоимость потока платежей больше нуля ( NPV > 0) , то в течение его срока проект возместит первоначальные затраты и обеспечит прибыль.

Отрицательный NPV означает, что норма доходности не указана и проект убыточный. При NPV = 0 проект оплачивает только затраты, но не приносит дохода. Однако у такого проекта есть свои аргументы в пользу — если он будет реализован, объем производства увеличится, то есть увеличится масштаб компании.

8.3. Формула расчета NPV

Для денежного потока, состоящего из N периодов (шагов), можно записать:

FC = FC₁ + FC₂ + … + FC_N,

Где:

FC – полный денежный поток

FC₁ и т.д. – денежные потоки всех периодов

NPV = FC₁/ (1 + D) + FC₂/ (1 + D) 2 + FC₃/ (1 + D) 3…………..и т.д.

Где D — ставка дисконтирования. Она отражает скорость изменения стоимости денег со временем, чем больше ставка дисконтирования, тем больше скорость.

8.4. Расчет дисконтирования

Дисконтирование — это приведение всех денежных потоков (потоков платежей) к единому моменту времени. Дисконтирование является базой для расчетов стоимости денег с учетом фактора времени.

Формула для расчета дисконтирования:

PV=FV*1/(1+i) n

Где:

PV — приведенная к настоящему времени ценность выгод или издержек

FV — будущая ценность выгод или издержек

i — ставка процента или коэффициент дисконтирования в текущем или реальном выражении

n — число лет или срок службы проекта

8.5. Ставка дисконтирования

Ставка дисконтирования (коэффициент дисконтирования)- это процентная ставка, используемая для перерасчета будущих потоков доходов в единую величину текущей стоимости. Ставка дисконтирования применяется при расчёте дисконтированной стоимости будущих денежных потоков NPV.

PV — первоначальная сумма.FV — наращенная сумма.I = (FV — PV) — процентные деньги, проценты.

Формула процентной ставки:

r = I/PV = (FV-PV)/PV

Процентная ставка — это сумма, указанная в процентах от суммы кредита, уплаченной получателем кредита за использование ее в течение определенного периода времени (месяц, квартал, год).

Как правило, процентная ставка известна из условий финансовой транзакции (например, из условий депозитного или кредитного договора), а затем из начисленной суммы вы можете написать:

FV = PV*(1+r).

Поэтому, зная процентную ставку и начальную сумму, мы определяем совокупную сумму.

Формула для расчета учетной ставки:

d = I/FV = (FV-PV)/FV

Зная ставку дисконтирования и накопленную сумму, мы решаем проблему скидок (определяем начальную сумму):

PV = FV*(1-d).

Учетная ставка и процентная ставка связаны со следующими факторами:

r = d * (FV/PV)d = r * (PV/FV)

Кроме того, т.к. процентная ставка определяется по отношению к начальной сумме, а ставка дисконтирования — к наращенной, процентная ставка больше ставки дисконтирования.

Варианты вложений

Существует три способа распоряжения денежными средствами проекта: расходование, сбережение, инвестиционный. Самым простым, но не самым доходным вариантом является вложение средств в банк, покупку долговых обязательств или банковских акций, свободно обращающихся на финансовой бирже.

Однако лучшим инвестиционным шагом будет вложение в расширение собственного бизнеса. Это подразумевает покупку долгосрочных финактивов (ОС или основных средств), использование которых в торговых или производственных процессах сформирует стабильные финансовые поступления.

Для определения успешности определённого инвестиционного проекта, бизнес-экспертами применяются конкретные методики анализа бизнес-планов. В оценке используются два ключевых механизма:

• IRR, иначе InternalRate of Return в переводе с английского — внутренняя норма доходности;
• NPV или Net PresentValue — чистая приведённая стоимость.

Значение ставки дисконтирования при расчёте NPV

Изучая чистую приведённую стоимость обязательно следует уделять серьёзное внимание показателю — ставка дисконтирования. Часто её именуют иначе — альтернативной стоимостью вложений

Показатель, используемый в формуле расчёта, обозначает минимальную величину доходности, которую инвестор считает для себя приемлемой при рисках, сопоставимых с имеющимися у реализуемого проекта.

Инвестор может оперировать средствами, привлекаемыми из различных источников (собственных либо заёмных).

1. В первом случае устанавливаемая ставка дисконтирования, является личной оценкой допустимых рисков рассматриваемого инвестиционного проекта.

Её оценка может иметь несколько подходов. Самые простые, это:

Выбор безрисковой ставки, корректируемой с учётом вероятности возникновения специфических рисков.

В качестве таковой обычно рассматриваются доходность по ценным бумагам государства, в котором реализуется проект, ставка доходности по корпоративным облигациям компаний отрасли.

Необходимая и минимально достаточная (с точки зрения потенциального инвестора) рентабельность (показатель ROE).

При этом, лицо, принимающее решение об инвестировании, определяет ставку дисконтирования по одному из возможных вариантов:

• в проект вкладываются средства, имеющиеся на депозите в конкретном банке. Следовательно, альтернативная стоимость не должна быть меньше имеющейся банковской ставки;
• В проект инвестируются средства, выведенные из бизнеса и являющиеся временно свободными. В случае возникновения потребности в них, оперативное изъятие всей суммы из проекта невозможно. Потребуется кредит. Поэтому в качестве текущей стоимости средств выбирается рыночная кредитная ставка;
• Средняя доходность основного бизнеса составляет Y%. Соответственно от инвестиционного проекта требуется получать не меньше.

2. При работе с заёмными средствами ставка будет рассчитана как величина производная от стоимости привлекаемых из различных источников средств.

Как правило ставка, устанавливаемая инвестором, в подобных случаях превышает аналогичный показатель стоимости заёмных денежных средств.

При этом не просто учитывается изменение стоимости средств во времени, но и закладываются возможные риски, связанные с неопределённостью поступления денежных потоков и их объёмов.

Это является главной причиной, по которой ставкой дисконтирования считают средневзвешенную стоимость привлекаемого для последующего инвестирования капитала (WACC).

Именно этот показатель рассматривается в качестве требуемой нормы доходности на средства, вложенные в конкретный инвестиционный проект.

Чем выше ожидаемые риски, тем выше ставка.

Расчётные методы определения данного параметра менее наглядны, чем графические. Особенно когда требуется сравнить привлекательность двух или более проектов.

Например, сравнивая проекты «А» и «Б» (смотри график) можно сделать следующие выводы:

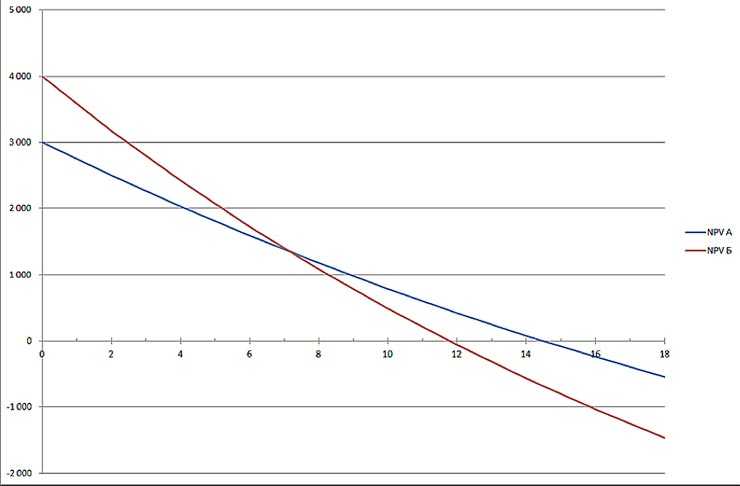
При ставке, превышающей значение 7%, величина NPV проекта А выше, чем у Б (что предупреждает о возможной ошибке в выборе при арифметическом сопоставлении).

К тому же инвестиционный проект «Б», обозначенный на графике красной кривой, подвержен более значительным изменениям в связи с изменяющейся ставкой дисконтирования (такое может быть объяснено разновеликими величинами поступающих средств в одинаковый период времени).

Следует учитывать факт существенного снижения величины ставок дисконтирования во времени, что накладывает определённые временные ограничение. Рассчитать их можно не более, чем за 10 лет.

Анализ графиков позволяет сделать вывод о том, что меняющаяся ставка дисконтирования приводит к изменениям величины показателя NPV (причём последний меняется нелинейно).

Поэтому для более взвешенной оценки необходимо не просто сравнивать величины для разных инвестиционных проектов, но и учитывать изменения последних при разных величинах ставки.

По умолчанию при расчете в Excel, ставка дисконтирования принимается равной 10%.

Расчет NPV в Excel

Чтобы проиллюстрировать как рассчитывается NPV в Excel, рассмотрим предыдущий пример заведя его в таблицы. Расчет можно произвести двумя способами

1. В Excel имеется формула ЧПС, которая рассчитывает чистую приведенную стоимость, для этого вам необходимо указать ставку дисконтирования (без знака проценты) и выделить диапазон чистого денежного потока. Вид формулы такой: = ЧПС (процент; диапазон чистого денежного потока).
2. Можно самим составить дополнительную таблицу, где продисконтировать денежный поток и просуммировать его.

Ниже на рисунке мы привели оба расчета (первый показывает формулы, второй результаты вычислений):

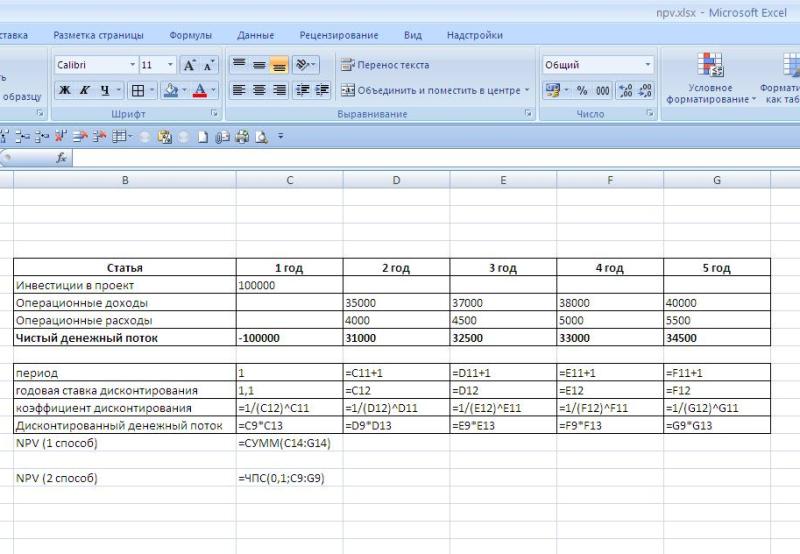
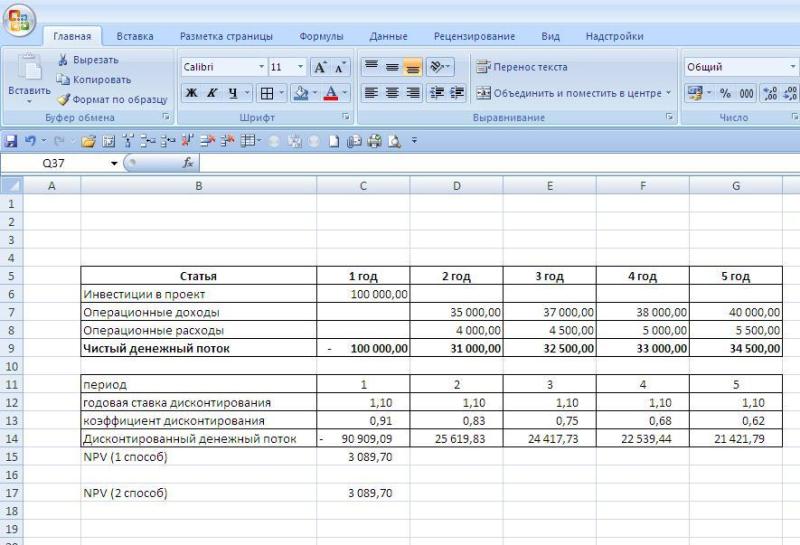
Как вы видите, оба метода вычисления приводят к одному и тому же результату, что говорит о том, что в зависимости от того, чем вам удобнее пользоваться вы можете использовать любой из представленных вариантов расчета.

Как рассчитать приведенную стоимость

Очевидно, 330 тыс.долл., которые мы получим в будущем, стоят дешевле 330 тыс. долл., которыми мы располагаем сегодня. И дело не только в инфляции.

Основная причина такого положения вещей в том, что мы можем имеющиеся 330 тыс. долл. инвестировать в безрисковые финансовые инструменты наподобие банковских депозитов или государственных облигаций.

В таком случае для определения «истинной» стоимости наших 330 тыс. долл. к ним требуется присовокупить еще и процентный доход по соответствующему депозиту (ценной бумаге).

На эту ситуацию можно посмотреть так: сегодняшние 330 тыс. долл. будут стоит в будущем столько же плюс – процентный доход по безрисковым финансовым инструментам.

Мы вплотную приблизились к пониманию одного из важнейших принципов теории инвестирования: деньги СЕГОДНЯ стоят ДОРОЖЕ, чем деньги, которые мы получим ЗАВТРА.

Именно поэтому приведенная стоимость любого дохода в будущем будет МЕНЬШЕ его номинального значения, и чтобы его найти, нужно ожидаемый доход умножить на некоторый коэффициент, заведомо МЕНЬШИЙ единицы.

Обычно этот коэффициент именуется коэффициентом дисконтирования.

Математическая запись нашего постулата будет иметь следующий вид:

PV = DF * C₁, где

PV – приведенная стоимость (от англ. present value),

DF – коэффициент (или – фактор) дисконтирования (от англ. discount factor),

C₁ – ожидаемый через 1 год доход.

Сущность коэффициента дисконтирования может быть истолкована так: это нынешняя стоимость 1 доллара, который мы рассчитываем получить в будущем. Численно он будет равен следующему отношению:

DF = 1 / (1 + r), где

r – размер вознаграждения (норма доходности), на который вправе рассчитывать инвестор в связи с отсрочкой получения дохода.

Итак, мы готовы к тому, чтобы рассчитать, наконец, приведенную стоимость будущих доходов от наших инвестиций.

Для этого введем в условия задачи размер процентной ставки по безрисковым финансовым инструментам, равный, к примеру, 8 процентам годовых.

В таком случае ставка дисконтирования будет равняться значению дроби 1 / (1 + 0,08):

DF = 1 / (1 + 0,08) = 1 / 1,08 = 0,926.

Приведенную стоимость 330 тыс. долл. мы рассчитаем так:

PV = DF * C₁ = 0,926 * 330 000 долл. = 305 580 долл.

Зависимость NPV проекта от ставки дисконтирования

Понятно, что получить абсолютно точные величины всех денежных потоков проекта и точно определить стоимость капитала, т.е. ставку дисконтирования невозможно. В этой связи интересно проанализировать зависимость NPV от этих величин. У каждого проекта она будет разная. Наиболее часто делается анализ чувствительности показателя NPV от стоимости капитала. Давайте рассчитаем NPV по проектам A и B для разных ставок дисконтирования:

Стоимость капитала, %	NPV A	NPV B
$3,000	$4,000
2	$2,497.4	$3,176.3
4	$2,027.7	$2,420.0
6	$1,587.9	$1,724.4
8	$1,175.5	$1,083.5
10	$788.2	$491.5
12	$423.9	($55.3)
14	$80.8	($562.0)
16	($242.7)	($1,032.1)
18	($548.3)	($1,468.7)

Таблица 3.  Зависимость NPV от ставки дисконтирования.

Табличная форма уступает графической по информативности, поэтому гораздо интереснее посмотреть результаты на графике (нажать, чтобы увеличить изображение):

Рисунок 3. Зависимость NPV от ставки дисконтирования.

Из графика видно, что NPV проекта A превышает NPV проекта B при ставке дисконтирования более 7% (точнее 7,2%). Это означает, что ошибка в оценке стоимости капитала для компании-инвестора может привести к ошибочному решению в плане того, какой проект из двух следует выбрать.

Кроме того, из графика также видно, что проект B является более чувствительным в отношении ставки дисконтирования. То есть NPV проекта B уменьшается быстрее по мере роста этой ставки. И это легко объяснимо. В проекте B денежные поступления в первые годы проекта невелики, со временем они увеличиваются. Но коэффициенты дисконтирования для более отдаленных периодов времени уменьшаются очень значительно. Поэтому вклад больших денежных потоков в чистую приведенную стоимость так же резко падает.

Например, можно рассчитать, чему будут равны $10,000 через 1 год, 4 года и 10 лет при ставках дисконтирования 5% и 10%, то наглядно можно увидеть, как сильно зависит приведенная стоимость денежного потока от времени его возникновения.

Таблица 4. Зависимость NPV от времени его возникновения.

Год	Ставка 5%	Ставка 10%	Разница, $	Разница, %
1	$9,524	$9,091	$433	4.5%
4	$8,227	$6,830	$1,397	17.0%
10	$6,139	$3,855	$2,284	37.2%

В последнем столбце таблицы видно, что один и тот же денежный поток ($10,000)  при разных ставках дисконтирования отличается через год всего на 4.5%. Тогда как тот же самый по величине денежный поток, только через 10 лет от сегодняшнего дня при дисконтировании по ставке 10% будет на 37.2% меньше, чем его же приведенная стоимость при ставке дисконтирования 5%. Высокая стоимость капитала «съедает» существенную часть дохода от инвестиционного проекта в отдаленные годовые периоды, и с этим ничего не поделать.

Именно поэтому, при оценке инвестиционных проектов денежные потоки, отстоящие от сегодняшнего дня более, чем на 10 лет, обычно не используются. Помимо существенного влияния дисконтирования, еще и точность оценки отдаленных по времени денежных потоков существенно ниже.

Просмотры:
24 309

Достоинства и недостатки метода

Несмотря на такие преимущества метода, как учёт изменения стоимости денежных средств с течением времени и учёт рисков, следует помнить о ряде ограничений:

• Все показатели, используемые в расчётах, носят прогнозный характер и остаются стабильными на протяжении всего срока реализации программы. В действительности же они могут значительно изменяться от заданных значений, что делает итоговую величину лишь вероятностным параметром.
• Ставки дисконтирования часто корректируются с учётом возможных рисков, что не всегда оправдано и приводит к необоснованному понижению конечного значения ЧПС. В связи с этим инвестор может отказаться от реализации прибыльного проекта.

Таким образом, метод расчёта NPV позволяет легко и качественно оценить вероятную прибыльность инвестиций, приведённую к текущему моменту времени.

Однако стоит помнить, что данная методика носит прогнозный характер и пригодна только при стабильной экономической ситуации.

Чистый дисконтированный доход это

Чистый дисконтированный доход (Чистая приведённая стоимость, Чистая текущая стоимость, Net present value, NPV) — это денежный поток, приведенный к текущей дате с использованием ставки дисконтирования.

А теперь, простыми и доступными словами. Если инвестиционный проект не в варианте «авось клево выйдет», то обычно заранее известны прогнозируемые издержки и доходы от месяца к месяцу или от года к году (допустим, средние продажи аналогов с учетом ряда факторов, таких как популярность товара или услуги).

Например, в первом периоде +100, во втором -200, в третьем +400 и так далее. Эти цифры вероятностны и весьма разрознены (в одном периоде плюс, в ином минус; в одном больше доход, в ином меньше), но их как-то можно анализировать. Иными словами, речь о предполагаемых денежных потоках.

Так же никого не удивишь тем, что деньги обесцениваются (инфляция, девальвация и прочее). Поэтому необходимо соотносить будущие прибыли с текущими ценами и возможностями. Например, стоимость растительного масла за 10 лет выросла примерно в 2 раза. Это значит, что за 1000 рублей 10 лет назад можно было приобрести в 2 раза больше масла.

Кроме того, от вложений ждут, что они не только позволят сохранить реальную стоимость капитала, но и принесут хотя бы небольшую прибыль. Иными словами, речь о ставке дисконтирования.

Суммируя вышесказанное, поэтому у инвесторов возникла идея, а что если все потоки денег соотнести с процентом дисконта и сложить. Тогда можно будет увидеть как по отношению к текущему моменту изменится сумма. А учитывая еще специфику ставки дисконтирования, так же можно будет увидеть насколько более выгоден или невыгоден проект.

Ремарка для читателей. Немного сложно звучит, но далее станет более понятно, о чем идет речь.