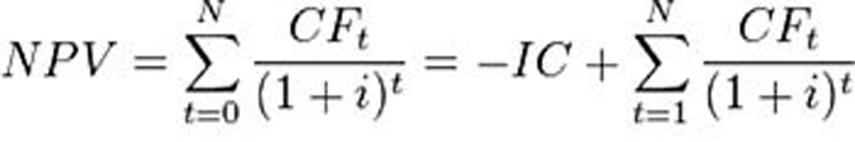Что такое чистый дисконтированный доход в экономике и бухгалтерии

Расчет

ЧДД рассчитывается как сумма имеющихся результатов и затрат в течение целого периода исследования, приведенная к первому шагу. Расчет предполагает, что норма дисконтирования является удовлетворительной для инвестора ставкой доходности на каждый рубль вложенного капитала по неопасному методу вложения.

Норма дисконтирования должна быть объективно оправдана, ведь учитываются:

• проценты по депозитам банков;
• средний доход ликвидных ценных бумаг;
• величина инфляции;
• личные оценки инвестора, сформированные на его познаниях и практическом опыте;
• стоимость капиталовложений, когда финансируется проект из многих источников.

Выбирая проект с NPV < 0, инвестор лишится части своих денег.

Порядок определения ЧДД такой:

1. Устанавливается настоящая стоимость расходов для исполнения проекта – величина инвестиций.
2. Устанавливается настоящая стоимость ожидаемых денежных течений от проекта путем расчета денежных вливаний.
3. Устанавливается текущая стоимость всех сумм предстоящих поступлений средств от проекта по причине ставки дисконтирования времени возникновения доходов.
4. Настоящая величина трат сопоставляется с суммарной имеющейся стоимостью доходов.

Чистый дисконтированный доход: формула расчета

NPV (ЧДД) = – IC + ƩCFt/ (1 + i)t, где t = 1…n.

Проанализируем, что обозначают компоненты этой формулы:

• IC – начальные вложения, иначе говоря, запланированные инвестиции в проект. Их вносят со значком минус, это траты вкладчика для реализации идеи, какая, как ожидается, принесет доход в будущем. Поскольку вклады часто производятся не в один момент, а по мере надобности, они дисконтируются с учетом временного интервала.
• CFT – денежные вливания, дисконтированные с учетом временных ресурсов. Его определяют как сумму вложений и расходов в каждый период t (меняется от 1 до n, где n-продолжительность инвестиционного бизнес-проекта).
• i – это значение ставки дисконта. Ее используют для дисконтирования предполагаемых доходов в единый размер стоимости на этот момент.

Ранее уже рассказывалось, что чистый приведенный доход считается типовым способом оценки результативности определенного проекта. Показатели этого индекса влияют на привлекательность проекта для инвестора.

NPV > 0

Как уже объяснялось, чистый приведенный доход относится к методам оценки результативности проекта. О чем говорит ЧДД, если при расчете он больше чем «0»? Эта ситуация сообщает о том, что относительно вклада, этот проект может быть выгодным. Однако конечное решение о финансировании принимают лишь после определения ЧДД всех проектов, какие участвовали в сравнении. Выбор (при других равных) должен быть один, где больше ЧДД.

NPV = 0

Иногда случается, что дисконтированный доход равняется нулю. Иначе говоря, с учетом временного фактора, вкладчик не лишится ничего, но и не сможет зарабатывать. Как правило, подобные проекты не принимаются, лишь в исключительных случаях.

NPV < 0

Когда при расчете чистой приведенной стоимости бизнес-идеи получается минусовое значение, в таком случае инвестиции не дадут прибыли. Значит, выбирая проект с NPV < 0, инвестор лишится части своих денег. Здесь все решается очень просто – отказывают в финансировании.

Пример

Корпорация должна решить, следует ли вводить новые линейки продуктов. Новый продукт будет иметь расходы на запуск, эксплуатационные расходы, а также входящие денежные потоки в течение шести лет.
Этот проект будет иметь немедленный (T = 0) отток денежных средств в размере $ 100 000 (которые могут включать в себя механизмы, а также расходы на обучение персонала). Другие оттоки денежных средств за 1-6 лет ожидаются в размере $ 5000 в год. Приток денежных средств, как ожидается, составит $ 30 000 за каждый год 1-6. Как только компания получает прибыль от реализации проекта (например, $ 25 000 после первого года), она кладёт их в банк под 10 % годовых на оставшееся до конца проекта время (то есть на оставшиеся 5 лет для первых $ 25 000). Все денежные потоки после уплаты налогов, и на 7 год никаких денежных потоков не планируется. Ставка дисконтирования составляет 10 %.

Таким образом, требуется оценить, какая сумма больше:

100000⋅(1+0.1)t≶∑i=1tpi⋅(1+0.1)(t−i){\displaystyle 100\,000\cdot (1+0.1)^{t}\lessgtr \sum _{i=1}^{t}p_{i}\cdot (1+0.1)^{(t-i)}}, где pi{\displaystyle p_{i}} — доход от проекта, полученный в i-й год реализации проекта, t — общая длительность проекта. Поделим обе части на (1+0.1)t{\displaystyle (1+0.1)^{t}}:

100000≶∑i=1tpi⋅(1+0.1)(−i){\displaystyle 100\,000\lessgtr \sum _{i=1}^{t}p_{i}\cdot (1+0.1)^{(-i)}}.

Каждое слагаемое в правой части неравенства — это приведённая стоимость денег по годам. Например, $ 25 000, полученные от реализации проекта после первого года и положенные в банк на 5 лет, дадут такой же доход, как $ 22 727, положенные в банк в начальный момент времени на 6 лет. Таким образом, приведённая стоимость (PV) может быть рассчитана по каждому году:

Год	Денежный поток	Приведённая стоимость
T=0	−100000(1+0.10){\displaystyle {\frac {-100\,000}{(1+0.10)^{0}}}}	– $ 100 000
T=1	30000−5000(1+0.10)1{\displaystyle {\frac {30\,000-5000}{(1+0.10)^{1}}}}	$ 22 727
T=2	30000−5000(1+0.10)2{\displaystyle {\frac {30\,000-5000}{(1+0.10)^{2}}}}	$ 20 661
T=3	30000−5000(1+0.10)3{\displaystyle {\frac {30\,000-5000}{(1+0.10)^{3}}}}	$ 18 783
T=4	30000−5000(1+0.10)4{\displaystyle {\frac {30\,000-5000}{(1+0.10)^{4}}}}	$ 17 075
T=5	30000−5000(1+0.10)5{\displaystyle {\frac {30\,000-5000}{(1+0.10)^{5}}}}	$ 15 523
T=6	30000−5000(1+0.10)6{\displaystyle {\frac {30\,000-5000}{(1+0.10)^{6}}}}	$ 14 112

Сумма всех этих значений является настоящей чистой приведённой стоимостью, которая равна $ 8881.52. Поскольку NPV больше нуля, то было бы лучше инвестировать в проект, чем класть деньги в банк (под 10 % годовых с капитализацией процентов), и корпорации должны вкладывать средства в этот проект, если нет альтернативы с более высоким NPV.

Тот же пример с формулами в Excel:

• NPV (ставка, net_inflow) + initial_investment
• PV (ставка, year_number, yearly_net_inflow)

При более реалистичных проблемах необходимо будет рассмотреть другие факторы, как расчет налогов, неравномерный денежный поток и ценности, а также наличие альтернативных возможностей для инвестиций.

Кроме того, если мы будем использовать формулы, упомянутые выше, для расчёта NPV — то мы видим, что входящие потоки (притоки) денежных средств являются непрерывными и имеют такую же сумму; и подставив значения в формулу

1−(1+i)−ni{\displaystyle {\frac {1-(1+i)^{-n}}{i}}} мы получим 1−(1+0.1)−60.1=4.3553{\displaystyle {\frac {1-(1+0.1)^{-6}}{0.1}}=4.3553}.

И если умножить полученное значение на денежные потоки (CF), и учесть первоначальные затраты, то в итоге вычислим чистую приведённую стоимость (NPV):

4.3553(30000−5000)−100000=$8881.52{\displaystyle -100\,000=\$\,8\,881.52}

Поскольку NPV больше нуля, то было бы лучше инвестировать в проект, чем ничего не делать, и корпорации должны вкладывать средства в этот проект, если нет альтернативы с более высоким NPV.

Какую ставку использовать для дисконтирования

При расчете показателей эффективности проекта, и чистого дисконтированного дохода в том числе, инвестор рано или поздно сталкивается с проблемой выбора ставки дисконтирования.

Однозначно правильного ответа, какую ставку дисконтирования использовать, нет. Но есть рекомендации согласно здравому смыслу, ведь желаемая ставка – это норма прибыли для инвестора с учетом всех рисков проекта.

Допустим, у инвестора имеется три альтернативных способа вложить имеющиеся средства:

1. Открыть вклад в банке.
2. Инвестировать в акции «голубой фишки».
3. Инвестировать в ИТ-стартап.

Понятно, что риски нарастают от первого варианта к третьему, значит, здравый инвестор будет требовать более высокой доходности от третьего вложения, чем от второго и тем более от первого. Но насколько более высокой?

Есть несколько подходов к определению ставки дисконтирования:

1. Учет только показателя инфляции. Такой подход работает в основном для безрисковых и низкорисковых вложений и используется редко.
2. Интуитивный, основанный на опыте инвестора. Подход не научный, но используется часто, требует минимальных затрат времени, поэтому имеет право на существование.
3. Приравнивание ставки дисконтирования к стоимости капитала инвестора (WACC). Средневзвешенный капитал инвестора состоит из уже имеющихся проектов (бизнесов) и приносит какую-то доходность. Использование WACC означает, что инвестор сравнивает доходность от рассматриваемого проекта с доходностью уже проведенных инвестиций.
4. Расчет ставки дисконтирования на основании прошлых периодов с использованием прогнозирования по линиям трендов. Работает, только если есть накопленная статистика по похожим проектам. Фактически для расчета берется динамика ставки дисконта на рынках схожих инвестиций минимум за три года и формируется обоснованный прогноз.
5. Для уникальных инвестиций, по которым нет еще накопленного опыта и высоки риски, используется метод расчета с учетом рисков. На практике этот метод используется наиболее часто, так как у редкого инвестора есть статистические данные по аналогичным вложениям. Поэтому остановимся на нем подробнее.

Формула расчета ставки дисконтирования с учетом рисков:

Где i – барьерная ставка

iб – безрисковая ставка, минимальная прибыль, которую хочет получить инвестор в условиях отсутствия рисков

N – количество рисков

n– порядковый номер риска

Rn – премия за n-ный номер риска

Перед проведением расчета необходимо перечислить и взвесить все риски проекта: производственные, финансовые, коммерческие, политические, технологические и прочие. «Взвесить» означает присвоить каждому риску коэффициент. Критическим рискам присваивается самый высокий коэффициент, серьезным – ниже ит.д. Сумма коэффициентов по всем рискам должна быть равна единице.

В результате проведения расчета вы получите обоснованную ставку, по которой будете производить дисконтирование денежных потоков проекта.

Что такое чистый дисконтированный доход (ЧДД)

При оценке инвестиционной привлекательности отдельных финансовых инструментов или целых проектов применяется показатель именуемый чистым дисконтированным доходом. При его упоминании часто используют аббревитуру ЧДД, а в английской транскрипции его называют Net Present Value (NPV).

Говоря простыми
словами, ЧДД представляет собой итог
всех денежных поступлений в рассматриваемый
инвестиционный проект и оттоков из
него. Эта величина наглядно показывает
инвестору есть ли перспективы у
конкретного инвестпроекта (в плане
получения прибыли) и стоит ли в него
вкладываться.

Дисконтирование
в данном случае позволяет привести все
денежные потоки к одному моменту времени.

Анализ
инвестиционного проекта при расчёте
ЧДД включает в себя несколько основных
этапов:

1. Оценка входящих
   и исходящих денежных потоков в плане
   результативности (эффективности). А
   именно – с точки зрения тех результатов,
   к которым приводят очередные вложения;
2. Определение
   ставки дисконтирования;
3. Дисконтировать
   все денежные потоки согласно установленной
   ставке;
4. Суммировать
   продисконтированные денежные потоки
   и получить в итоге величину ЧДД.

Существует три основных
значения ЧДД:

1. Положительное
   (ЧДД>0);
2. Отрицательное
   (ЧДД<0);
3. Нейтральное
   (ЧДД=0).

ЧДД>0 говорит о том, что положительные денежные потоки превалируют над отрицательными и свидетельствует об инвестиционной привлекательности рассматриваемого проекта;

ЧДД<0, напротив, говорит о том, что отток капитала превышает величину поступлений денежных средств и предупреждает инвестора о потенциальной убыточности рассматриваемого проекта;

ЧДД=0 показывает инвестору относительную нейтральность анализируемого проекта. Он не приносит ни прибыли, ни убытка. Вкладываться в такой проект стоит лишь при наличии другой заинтересованности (помимо получения прибыли), например если дело касается спонсорской поддержки или каких-либо социально значимых проектов.

Определение
ставки дисконтирования

Определение
максимально достоверной ставки
дисконтирования — процесс довольно
сложный, требующий объективного
кропотливого анализа множества
составляющих рассматриваемого проекта.

В самом общем
случае при этом необходимо учитывать
следующие показатели:

• Уровень
  инфляции (текущий и в динамике);
• Проценты
  получаемые по вкладам;
• Средний
  процент доходности получаемой от ценных
  бумаг;
• Прогнозируемые
  аналитиками данные по будущей доходности;
• Общая стоимость
  всех вложений в проект и уровень
  вовлечённости в него других инвесторов.

Формула и пример
расчёта ЧДД

Для расчёта
величины чистого дисконтированного
дохода используют следующую формулу:

Чтобы не быть
голословным, я приведу простой пример
расчёта величины ЧДД исходя из данных
гипотетического инвестиционного проекта
величина денежных потоков по которому
приведена в нижеследующей таблице.

Год (порядковый номер)	Величина денежного потока, млн рублей
100
1	-150
2	200
3	300

Предположим,
что значение ставки дисконтирования в
данном случае равно 10%. Тогда расчёт
будет выглядеть следующим образом:

100/(1+0,1)^0
+ (-150)/(1+0,1)^1 + 200/(1+0,1)^2 + 300/(1+0,1)^3 = 322,11

Полученное
положительное значение ЧДД говорит о
способности рассматриваемого проекта
генерировать прибыль. В приведённом
примере всё просто и понятно, ведь он
не включает в себя весь спектр
предварительных работ и расчётов –
ставка дисконтирования уже рассчитана
и величины денежных потоков определены.
Это теория, а в реальности всё конечно
сложнее.

Надо понимать,
что при расчётах реальных инвестпроектов
следует использовать только достоверную,
тщательно выверенную информацию.

Выбор ставки для расчета

При определении эффективности проекта инвестор должен выбрать подходящую ставку дисконтирования. Невозможно точно сказать, какой показатель подходит для той или иной ситуации, но опытные инвесторы рекомендуют воспользоваться нормой прибыли для вкладчика, учитывая возникающие риски. При определении ставки используется несколько подходов:

• учет уровня инфляции, хотя этот показатель важен при выборе проектов с низким или средним уровнем риска;
• интуитивный подходит для бывалых инвесторов, а также для определения показателя не нужно тратить много времени, хотя часто даже опытные предприниматели совершают ошибки;
• учет стоимости капитала, состоящего из текущих проектов, приносящих доход, что позволяет сравнить доходность нового проекта с прибыльностью других бизнесов;
• использование показателей прошлых периодов, но этот подход работает исключительно при выборе однотипных проектов. А также используются показатели минимально за 3 года работы;
• метод с учетом риска, применяемый для уникальных вложений, по которым наблюдается высокий уровень риска.

Каждая методика имеет свои плюсы и минусы, причем опытные инвесторы часто предпочитают пользоваться сразу несколькими вариантами.

Для чего необходимо дисконтирование и что это вообще такое

Теперь мы с вами подошли
непосредственно к сути рассматриваемого
вопроса. Исходя из того, что стоимость
денег в разные моменты времени различна,
то каким образом можно свести воедино
множество платежей (денежных потоков)
произведённых в различные временные
промежутки? Ведь одна и та же сумма
платежей произведённых в разное время
будет оцениваться по разному.

Ответ на поставленный
вопрос, как вы уже конечно догадались
— дисконтирование денежных потоков.

Для того чтобы было
понятнее вот вам простой пример. Вам
должны определённую сумму денег и вам
их выдают по частям ежемесячно. Положим,
что сумма равна одному миллиону рублей,
а выдать её обязуются в течение года.
Самый очевидный способ разбивки
ежемесячных платежей будет разделить
миллион на двенадцать равных частей
(1000000/12=83333,33). Но этот способ, как вы уже
догадываетесь, не самый правильный,
ведь каждый месяц стоимость денег (того
самого миллиона рублей) будет неуклонно
падать и когда к концу года вы получите
всю сумму на руки, она будет стоить уже
гораздо меньше того, что стоила год
назад.

А вот если учесть
временную стоимость денег, то каждый
ежемесячный платёж должен учитывать
факт того, что деньги с каждым месяцем
дешевеют. Если за основу взять ставку
по банковским депозитам в 5%, то через
один месяц платёж должен составлять не
83333,33 рублей, а 83333,33+(5/12)%=83680,55 рублей.
Через два месяца: 83333,33+2*(5/12)%=84027,77 рублей
и т.д.

Вот именно этот процесс
приведения потоков платежей осуществляемых
в разное время к одному конкретному
моменту времени (в данном случае момент
возникновения задолженности) с учётом
конкретной ставки дисконтирования (в
данном случае 5%) и называется
дисконтированием.

До этого определения
мы добирались достаточно долго, но зато
теперь оно стало максимально для вас
понятным (по крайней мере хочется на
это надеяться).

Расчет NPV: формула

Определяется дисконтированный доход как разница между интегральными доходами и расходами, приведенная к нулевому периоду (сегодняшнему дню). Формула расчета ЧДД имеет следующий вид:

NPV (ЧДД) = — IC + ƩCF t / (1 + i) t , где t = 1…n.

Рассмотрим, что означают все составляющие данной формулы:

1. IC — первоначальные инвестиции, то есть планируемые вложения в проект. Они берутся со знаком минус, так как это затраты инвестора на реализацию бизнес-идеи, от которых ожидается получить отдачу в будущем. Так как инвестиции зачастую осуществляются не одномоментно, а по мере необходимости (распределены во времени), то их также следует дисконтировать с учетом временного фактора.
2. CF t — денежный поток, дисконтированный с учетом времени. Он определяется как сумма всех притоков и оттоков в каждом периоде t (изменяется от 1 до n, где n — длительность инвестиционного проекта).
3. i — это ставка дисконта (процента). Она применяется для дисконтирования всех ожидаемых поступлений в единое значение стоимости на текущий момент времени.

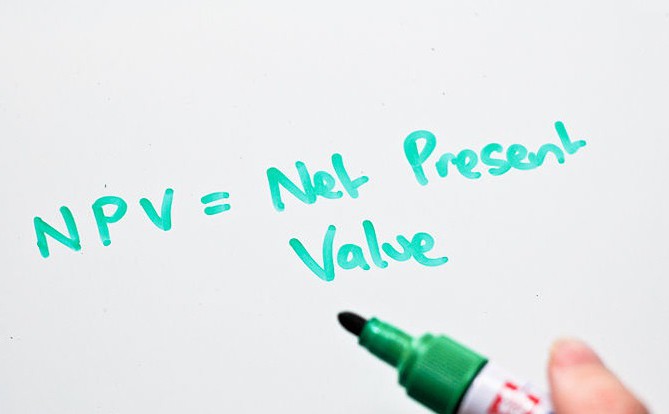
Пример расчета IRR в Excel

Быстро рассчитать IRR можно с помощью встроенной функции ВСД. Синтаксис:

• диапазон значений – ссылка на ячейки с числовыми аргументами, для которых нужно посчитать внутреннюю ставку доходности (хотя бы один денежный поток должен иметь отрицательное значение);
• предположение – величина, которая предположительно близка к значению ВСД (аргумент необязательный; но если функция выдает ошибку, аргумент нужно задать).

Возьмем условные цифры:

Первоначальные затраты составили 150 000, поэтому это числовое значение вошло в таблицу со знаком «минус». Теперь найдем IRR. Формула расчета в Excel:

Расчеты показали, что внутренняя норма доходности инвестиционного проекта составляет 11%. Для дальнейшего анализа значение сравнивается с процентной ставкой банковского вклада, или стоимостью капитала данного проекта, или ВНД другого инвестиционного проекта.

Мы рассчитали ВНД для регулярных поступлений денежных средств. При несистематических поступлениях использовать функцию ВСД невозможно, т.к. ставка дисконтирования для каждого денежного потока будет меняться. Решим задачу с помощью функции ЧИСТВНДОХ.

Модифицируем таблицу с исходными данными для примера:

Обязательные аргументы функции ЧИСТВНДОХ:

• значения – денежные потоки;
• даты – массив дат в соответствующем формате.

Формула расчета IRR для несистематических платежей:

Существенный недостаток двух предыдущих функций – нереалистичное предположение о ставке реинвестирования. Для корректного учета предположения о реинвестировании рекомендуется использовать функцию МВСД.

Аргументы:

• значения – платежи;
• ставка финансирования – проценты, выплачиваемые за средства в обороте;
• ставка реинвестирования.

Предположим, что норма дисконта – 10%. Имеется возможность реинвестирования получаемых доходов по ставке 7% годовых. Рассчитаем модифицированную внутреннюю норму доходности:

Полученная норма прибыли в три раза меньше предыдущего результата. И ниже ставки финансирования. Поэтому прибыльность данного проекта сомнительна.

Дисконтирование и компаундирование

Когда речь идёт о том,
чтобы соотнести все будущие денежные
потоки относительно настоящего момента
времени, то речь идёт о дисконтировании.
В тех же случаях когда, наоборот, денежные
потоки приводятся к определённой точке
в обозримом будущем — речь идёт уже о
компаундировании (или наращении) денежных
потоков.

Для простоты понимания
вот вам два примера.

Пример первый.
Дисконтирование

Допустим вы поставили
себе целью поездку на очередные
Олимпийские игры которые должны
состояться ровно через 4 года. Вы
подсчитали, что с учётом всех сопутствующих
расходов (билеты, проезд, проживание и
т.п.) вам потребуется сумма денег в 10000
долларов.

Сумма эта достаточно
серьёзная для того, чтобы просто взять
и вырвать её из своего семейного бюджета,
поэтому вы решаете позаботиться о её
накоплении заранее. Можно начать
ежемесячно откладывать деньги. А можно
рассчитать какую сумму денег необходимо
вложить в банк сейчас, чтобы через 4 года
размер вклада достиг требуемых 10000
долларов.

Допустим вы решили
вложить деньги в банк под 7% годовых.
Рассчитать требуемую сумму вклада при
этом можно умножив требуемые 10000$
на коэффициент дисконтирования
вычисляемый по формуле:

Подставляя в формулу
наши цифры и умножая на 10000 получим:

10000*(1/(1+0,07)^4))=7633,58$

То есть, для того чтобы
через четыре года получить требуемые
10000$ вам потребуется
вложить в банк 7635$.

Приведённый выше расчёт есть ни что иное как дисконтирование

Обратите внимание, что при его проведении мы двигались от денежных сумм в будущем к суммам в настоящем. Или, оперируя общепринятыми терминами, от будущей стоимости FV (Future Value) к стоимости текущей PV (Present Value)

Пример второй.
Компаундирование

Теперь рассмотрим
другой пример. Допустим у вас образовался
определённый излишек денежных средств,
которые вам вряд ли потребуются в
ближайшие пять лет и вы хотите их
приумножить ничем при этом практически
не рискуя. Самый безрисковый вариант в
данном случае опять же банковский
депозит.

Пускай у вас есть
средства в размере 5000$ которые
вы готовы вложить под 7% годовых на срок
в 5 лет. Прибыль от этого вклада можно
рассчитать умножив вкладываемую сумму
денег на коэффициент наращения вычисляемый
по формуле:

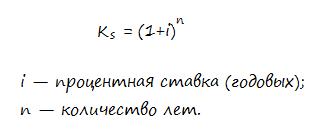
Подставим наши цифры,
умножим на 5000 и получим:

5000*(1+0,07)^5=7012,75$

То есть, в итоге
через пять лет сумма вклада вырастет
до 7012 долларов. В данном примере мы
рассмотрели с вами операцию наращения
или компаундирования в которой опять-таки
фигурировали две основные составляющие
в виде текущей и будущей стоимости:

• PV=5000 долларов;
• FV=7012,75
  долларов.

Обратите внимание на
то, что проводя данный расчёт мы с вами
двигались от денежных сумм в настоящем,
к суммам в будущем времени

Способы расчета ЧПС

При помощи чистого дисконт дохода проекта можно дать оценку инвестиционному КПД. Формула подсчёта чистой текущей стоимости бизнеса выглядит следующим образом:

, где:

N — число временных промежутков, за которые необходимо рассчитать инвестпроект;
t — время, за которое принимается чистый финпоток;
CF — ∑ чистых финпоступлений;
Программа Excel даёт возможность посчитать чистую текущую инвестиционную стоимость несколькими способами. Формула расчёта NPV будет работать только при корректно заданной ставке дисконта и выделенном «коридоре» NPV или ЧДП. Для начала работы в Excel выбирается вкладка «формула», после этого «финансовые» в заключении «ЧПС».В ячейке «аргументы функции» выбирают строку «Ставка» и указывают величину дисконтставки. В строчке «Значение 1» вписывают приведённые финансовые потоки NPV

Важно! В отмеченном диапазоне нужно отключить первую ячейку со стартовыми вложениями. Иначе чистый инвестиционный дисконтдоход проекта будет показывать неточный результат.

С использованием калькулятора

Дисконтная ставка проекта для NPV может быть рассчитана несколькими способами. К примеру, взять её эквивалентной рентабельности по минимальной инвестиционной доходности консервативных вложений средств. Или же принять в виде дисконта для NPV процентную ставку кредита либо индекс процентного преобразования величины цен за конкретный временной отрезок. «Ручной» мониторинг осуществляется поэтапно:

1. Считается сумма первоначальных капиталовложений (к ним относятся все денежные средства, которые инвестор планирует вложить на начальной стадии, в том числе непрямые затраты).
2. Выбирается временной отрезок (t) для инвестиционного анализирования.
3. Определяется финансовый поток проекта за все временные отрезки. Если необходимо найти чистый дисконтированный доход на 6 лет, то и инвестиционных финансовых потоков будет также 6. Между ними может быть разница по объёму, но они могут быть и одинаковыми.
4. Устанавливается дисконт ставка.
5. Уменьшаются финпотоки за каждый год на дисконтставку (дисконтирование финпоступлений).
6. Выполняется суммирование всех полученных инвестиционных дисконтпотоков. Из результата вычитается ∑ стартовых капиталовложений.

Произвести математический расчёт чистой текущей стоимости проекта довольно просто. Достаточно знать все переменные величины для определения чистого дисконтированного дохода. Но именно на этом этапе у большинства инвесторов возникают трудности.

Денежные потоки (CF)

На этом этапе необходимо знать предварительно ∑ всех притоков по инвестпроекту и расходы на него. Когда рассматривается процесс компании инвестора, то необходимо будет вычислять объем и ∑ предполагаемых продаж, а параллельно с этим, произвести достоверную калькуляцию всего бюджета проекта (арендная плата, сырьевые материалы, налоговые сборы, выплата заработной платы, логистика и пр.).

Анализируя потенциальные поступления, необходимо дать определение характеру и степени обусловленности между воздействием причин, формирующих инвестиционные финансовые потоки и самим заполнением денежных зачислений.

При положительном значении NPV инвестиционный проект станет прибыльным. Отрицательное значение NPV свидетельствует об убыточности проекта. Лучшим решением будет воздержаться от него или откорректировать первичные данные. Если величина NPV равна нулю, проект окупится, но получить прибыль не получится.

Для чего используется чистый дисконтированный доход

Показатель ЧДД – это главный фактор, на который инвестор обращает внимание, планируя свои инвестиции в ту или иную программу. Только расчета дисконтированного дохода принимается решение о целесообразности инвестиций

Выбирая проект для вложения собственных средств, инвестор должен проанализировать:

• срок инвестиции;
• сумму дохода;
• вид бизнеса.

А число ЧДД позволяет узнать реальную эффективность вашей инвестиции, упуская все вышеизложенные факторы. Благодаря этому показателю четко видно, какой из предложенных проектов может принести больше прибыли.

Кроме того, денежная сумма, которою вы сейчас собираетесь инвестировать, до окончания инвестиционного периода может иметь меньшею истинную стоимость, чем на данный момент. Также всегда существует риск, что, несмотря на подробные расчеты, ваши инвестиции могут не принести вам ожидаемой суммы прибыли.

Важные замечания

ЧДД обширно применяется в отечественной практической деятельности и при работе в других странах для установления результативности инвестиционных проектов. Так получают довольно отчетливое представление о рентабельности инвестиций. Преимуществом значения ЧДД считается то, что он измеряет видоизменение стоимости денежных вливаний во времени. Это помогает учитывать такие обстоятельства, как инфляцию, а кроме того сопоставлять разнообразные по длительности и частоте поступлений по проектам. Несмотря на ряд минусов, значение ЧДД является основным при оценке привлекательности бизнес-идеи, сопоставление с аналогами и конкурентами.

Для того чтобы инвестиции в определенный проект были обоснованными и подтверждались высокой рентабельностью, нужны достоверные исходные данные. Иными словами, такие виды планов, как производственный, маркетинговый или финансовый должны отображать информацию максимально близко к предстоящей реальности.

В частности, завышение предполагаемого спроса, при каком анализ ситуации приводит к положительному результату ЧДД, может в ходе исполнения проекта принести всем участникам убытки.

Одновременно с расчетом ЧДД надлежит рассчитать индекс доходности, какой может повлиять на решение кредиторов или инвесторов в пользу события с самым малым значением ЧДД, но с максимальным запасом прочности.

Определяя самый рентабельный вклад, освобожденный из бизнеса, вкладчик склоняется к более выгодному проекту. На основе высчитывания ЧДД текущей сопоставить некоторое количество возможностей с разнообразным временем окупаемости является более удобным.