Факторный метод экономического анализа

Методы факторного анализа. Основные этапы проведения факторного анализа

Методы факторного анализа

Факторный анализ – это методы комплексного и системного изучения и измерения воздействия факторов на величину результативного показателя.

Типы факторного анализа:

1.а) детерминированный (функциональный);

б) стохастический (корреляционный);

2.а) прямой (дедуктивный);

б) обратный (индуктивный);

3.а) одноступенчатый;

б) многоступенчатый;

4.а) статический;

б) динамический;

5.а) ретроспективный;

б) перспективный.

Основные этапы проведения факторного анализа:

1)отбор факторов, определяющих результативный показатель;

2)классификация и систематизация факторов;

3)определение формы зависимости;

4)моделирование взаимосвязей;

5)оценка влияния факторов на результативный показатель;

6)работа с факторной моделью.

Рассмотрим методы измерения влияния факторов в детерминированном анализе.

При моделировании детерминированных факторных систем необходимо соблюдать ряд требований:

1.Факторы, включенные в модель, и сами модели должны иметь определенно выраженный характер и реально существовать.

2.Факторы, входящие в модель, должны быть не только необходимыми элементами формулы, но и находиться в причинно-следственной связи с изучаемыми показателями.

3.Все показатели факторной модели должны быть количественно измеримыми.

4.Факторная модель должна обеспечивать возможность измерения влияния отдельных факторов. Это значит, что в ней должна учитываться соразмерность изменений результативного и факторных показателей, а сумма влияния отдельных факторов должна равняться приросту результативного показателя.

Наиболее часто в детерминированном анализе встречаются следующие модели:

1.Аддитивные модели:

У = å Х_i = Х₁ + Х₂ + … + Х_n.

Формирование этих моделей достигается за счет расчленения одного из факторных показателей на составные элементы.

2.Мультипликативные модели:

У = ПХ_i = Х₁´ Х₂´ … ´ Х_n.

Моделирование осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители.

3.Кратные модели:

У =	Х1	.
Х2

Кратные модели можно преобразовывать:

-удлинением;

-формальным разложением;

-расширением;

-сокращением (свертыванием).

Удлинение предусматривает преобразование числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей.

Себестоимость =	Затраты	=	Материалы	+	Труд	+	Амортизация	+	Накл. расходы	.
Количество	Количество	Количество	Количество	Количество

Способ формального разложения предусматривает удлинение знаменателя исходной факторной модели заменой одного или нескольких факторов на сумму или произведение однородных показателей.

Рентабельность продукции	=	Прибыль	=	Прибыль	.
Затраты	Материалы + Труд + Амортизация + Накл. расходы

Метод расширения предусматривает умножение числителя и знаменателя исходной модели на один или несколько новых показателей. Конечная модель будет содержать новый набор факторов.

Рентабель­ность про­дукции

=

Прибыль

=

Прибыль

´

Чистая выручка

=

Рентабель­ность продаж

´

Оборачивае­мость инве­стиций

= Х1´ Х2

.

Инвести­ции

Инвести­ции

Чистая выручка

Способ сокращения дает новую факторную модель путем деления числителя и знаменателя на один и тот же показатель.

Рентабельность инвестиций	=	Прибыль	=	Прибыль : Чистая выручка	=	Рентабельность продаж	.
Инвестиции	Инвестиции : Чистая выручка	Капиталоемкость продаж

4.Смешанные (комбинированные) модели:

У =	a
b – c

Статистическая модель

В подтверждающем факторном анализе исследователи обычно заинтересованы в изучении степени, в которой отклики на вектор наблюдаемых случайных величин p x 1 могут быть использованы для присвоения значения одной или нескольким ненаблюдаемым переменным η . Исследование в основном осуществляется путем оценки и оценки загрузки каждого элемента, используемого для выявления аспектов ненаблюдаемой скрытой переменной. То есть y — это вектор наблюдаемых ответов, предсказанных ненаблюдаемой скрытой переменной , которая определяется как:
ξ {\ displaystyle \ xi}

Y знак равно Λ ξ + ϵ {\ Displaystyle Y = \ Lambda \ xi + \ epsilon} ,

где — вектор p x 1 наблюдаемых случайных величин, — ненаблюдаемые скрытые переменные и — матрица p x k, где k равно количеству скрытых переменных. Так, несовершенные меры , модель также состоит из ошибок, . Оценки в случае максимального правдоподобия (ML), полученные путем итеративной минимизации функции соответствия,
Y {\ displaystyle Y} ξ {\ displaystyle \ xi} Λ {\ displaystyle \ Lambda} Y {\ displaystyle Y} ξ {\ displaystyle \ xi} ϵ {\ displaystyle \ epsilon}

F M L знак равно пер ⁡ | Λ Ω Λ ′ + я — диагональ ⁡ ( Λ Ω Λ ′ ) | + tr ⁡ ( р ( Λ Ω Λ ′ + я — диагональ ⁡ ( Λ Ω Λ ′ ) — 1 ) — пер ⁡ ( р ) — п {\ displaystyle F _ {\ mathrm {ML}} = \ ln | \ Lambda \ Omega \ Lambda {‘} + I- \ operatorname {diag} (\ Lambda \ Omega \ Lambda {‘}) | + \ operatorname {tr} (R (\ Lambda \ Omega \ Lambda {‘} + I- \ operatorname {diag} (\ Lambda \ Omega \ Lambda {‘}) ^ {- 1}) — \ ln (R) -p}

где — ковариационная матрица дисперсии, подразумеваемая предложенной моделью факторного анализа, а — наблюдаемая ковариационная матрица дисперсии. То есть находятся значения для свободных параметров модели, которые минимизируют разницу между подразумеваемой моделью ковариационной матрицей и наблюдаемой ковариационной матрицей дисперсии.
Λ Ω Λ ′ + я — диагональ ⁡ ( Λ Ω Λ ′ ) {\ displaystyle \ Lambda \ Omega \ Lambda {‘} + I- \ operatorname {diag} (\ Lambda \ Omega \ Lambda {‘})} р {\ displaystyle R}

Понятие факторного анализа

Факторный анализ – это многомерная методика, позволяющая изучить взаимосвязи между параметрами переменных. В процессе происходит исследование строения ковариационных или корреляционных матриц. Факторный анализ используется в самых различных науках: психометрике, психологии, экономике. Основы этого метода были разработаны психологом Ф. Гальтоном.

Как учетная политика влияет на прибыль?

Задачи проведения

Для получения достоверных результатов лицу требуется сравнить показатели по нескольким шкалам. В процессе определяется корреляция полученных значений, их сходство и различия. Рассмотрим базовые задачи факторного анализа:

• Обнаружение существующих значений.
• Подбор параметров для полноценного анализа значений.
• Классификация показателей для системной работы.
• Обнаружение взаимосвязей между результативными и факторными значениями.
• Определение степени влияния каждого из факторов.
• Анализ роли каждого из значений.
• Применение факторной модели.

Исследован должен быть каждый параметр, который влияет на итоговое значение.

Факторный анализ прибыли от продаж

Факторный анализ – это способ комплексного и системного измерения и исследования влияния факторов на размер итоговых показателей. Он осуществляется на основе бух. отчета по второй форме.

Главными факторами, которые влияют на размер прибыли, являются:

1. Объем продажи продукции. Чтобы узнать, как он влияет на доходность, нужно перемножить изменение количества реализованных товаров на прибыль прошлого периода отчета.
2. Разнообразие продаваемых товаров. Чтобы узнать его влияние, требуется сравнить прибыль текущего периода, которая рассчитана на основании себестоимости и цен базисного периода, с базисной прибылью, перерассчитанной на изменение количества проданных продуктов.
3. Изменение себестоимости. Чтобы узнать ее влияние, требуется сопоставить себестоимость реализации товаров периода отчета с издержками базисного периода, которые пересчитаны на изменение уровня реализации.
4. Издержки коммерческого и административного характера. Их влияние рассчитывается путем сравнения их размеров в базисном периоде и периоде отчета.
5. Уровень цен. Чтобы узнать его влияние, требуется сравнить уровень продаж периода отчета и базисного периода.

Этапы факторного анализа

Не важно, какой метод факторного анализа будет использован в процессе исследования. В любом случае, оно делится на несколько этапов:

В первую очередь, отбираются все факторы, которые могут повлиять на результат. Зачастую используют данные бухгалтерского учета

Однако допускается использование иных источников информации.
На следующем этапе важно классифицировать факторы по любому из удобных признаков. Например, по затратам, по экономическим показателям или по сезону.
После того, как все показатели отобраны и классифицированы, можно проводить анализ одним или несколькими методами

Для этого производят расчеты для каждого фактора по отдельности.
Следующий этап – нахождение взаимосвязи между показателями.
В заключение, на основании проведенного исследования делают вывод.

Факторный анализ прибыли от продаж – пример расчета

Исходная информация:

Показатель	Базисный период, тыс. руб.	Период отчета	Абсолютное изменение	Относительное изменение, %
Размер выручки	57700	54200	-3500	-6,2
Себестоимость товара	41800	39800	-2000	-4,9
Коммерческие затраты	2600	1400	-1200	-43,6
Административные издержки	4800	3700	-1100	-21,8
Прибыль	8500	9100	600	7,4
Изменение цен	1,05	1,15	0,10	15
Объем продаж	57800	47100	-10700	-18,5

Перечисленные выше факторы оказали на прибыль следующее влияние:

1. Объем проданной продукции – -1578 тыс. руб.
2. Разнообразие продаваемых товаров – -1373 тыс. руб.
3. Себестоимость – -5679 тыс. руб.
4. Коммерческие издержки – +1140 тыс. руб.
5. Административные издержки – +1051 тыс. руб.
6. Цены – +7068 тыс. руб.
7. Влияние всех факторов – +630 тыс. руб.

Исследовательский факторный анализ

И исследовательский факторный анализ (EFA), и подтверждающий факторный анализ (CFA) используются для понимания общей дисперсии измеряемых переменных, которая, как полагают, связана с фактором или латентной конструкцией. Однако, несмотря на это сходство, EFA и CFA представляют собой концептуально и статистически разные анализы.

Цель EFA — выявить факторы на основе данных и максимизировать объясненную дисперсию. От исследователя не требуется иметь никаких конкретных гипотез о том, сколько факторов возникнет, и какие элементы или переменные будут включать эти факторы. Если эти гипотезы существуют, они не учитываются и не влияют на результаты статистического анализа. Напротив, CFA оценивает априорные гипотезы и в значительной степени руководствуется теорией. Анализ CFA требует, чтобы исследователь заранее выдвинул гипотезу о количестве факторов, о том, коррелированы ли эти факторы, и какие элементы / меры влияют и отражают какие факторы. Таким образом, в отличие от исследовательского факторного анализа , где все нагрузки могут изменяться, CFA допускает явное ограничение определенных нагрузок равным нулю.

EFA часто считается более подходящим, чем CFA, на ранних этапах разработки шкалы, потому что CFA не показывает, насколько хорошо ваши элементы влияют на негипотетические факторы. Еще один веский аргумент в пользу первоначального использования ОДВ заключается в том, что неверное указание количества факторов на ранней стадии разработки шкалы, как правило, не будет обнаружено подтверждающим факторным анализом. На более поздних стадиях разработки шкалы подтверждающие методы могут предоставить больше информации за счет явного противопоставления конкурирующих структур факторов.

ОДВ иногда упоминается в исследованиях, когда CFA может быть лучшим статистическим подходом. Утверждалось, что CFA может быть ограничительным и неуместным при использовании в исследовательских целях. Однако идея о том, что CFA является исключительно «подтверждающим» анализом, иногда может вводить в заблуждение, поскольку индексы модификации, используемые в CFA, носят в некоторой степени исследовательский характер. Индексы модификации показывают улучшение соответствия модели, если конкретный коэффициент не ограничивается. Точно так же EFA и CFA не обязательно должны быть взаимоисключающими анализами; Утверждалось, что EFA является разумным продолжением плохо подходящей модели CFA.

3.4. Виды моделей. Моделирование

По характеру взаимосвязи между показателями различают методы детерминированного и стохастического факторного анализа.

Детерминированный факторный анализ представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер.

Основные свойства детерминированного подхода к анализу:

1. построение детерминированной модели путем логического анализа;
2. наличие полной (жесткой) связи между показателями;
3. невозможность разделения результатов влияния одновременно действующих факторов, которые не поддаются объединению в одной модели;
4. изучение взаимосвязей в краткосрочном периоде.

Моделирование — процесс представления исследуемого показателя с факторами, которое передается в форме конкретного математического уравнения.

Различают четыре типа детерминированных моделей.

1. Аддитивные модели представляют собой алгебраическую сумму показателей и имеют вид:

К таким моделям, например, относятся показатели себестоимости во взаимосвязи с элементами затрат на производство и со статьями затрат; показатель объема производства продукции в его взаимосвязи с объемом выпуска отдельных изделий или объема выпуска в отдельных подразделениях.

2. Мультипликативные   модели   в   обобщенном   виде   могут быть представлены формулой:

Примером мультипликативной модели является двухфакторная модель объема производства продукции:

где Ч — среднесписочная численность работников;
CB — средняя выработка на одного работника.

3. Кратные модели:

Примером кратной модели служит показатель срока оборачиваемости товаров (в днях) Т_ОБ.Т:

где З_Т — средний запас товаров;О_Р — однодневный объем реализации.

4. Смешанные модели представляют собой комбинацию перечисленных выше моделей и могут быть описаны с помощью специальных выражений:

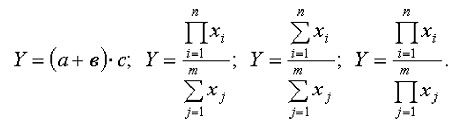
Примерами таких моделей служат показатели затрат на 1 руб. товарной продукции, показатели рентабельности и др.

Для изучения зависимости между показателями и количественного измерения множества факторов, повлиявших на результативный показатель, приведем общие правила преобразования моделей (моделирования) с целью включения новых факторных показателей.

Моделирование мультипликативных и аддитивных моделей осуществляется за счет разложения одного из факторных показателей на его сомножители:

A = a + b;                 b = c + d;                  A = a + c + d или

A = a * b;                   b = c * d;                   A = a * c * d

Степень детализации и расширения модели зависит от цели исследования, а также от возможностей детализации и формализации показателей в пределах установленных правил.

Кратные модели преобразуются следующими способами:

1. Удлинение.

.

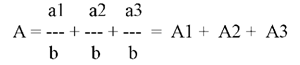
2. Формальное разложение.

b = b1 + b2 + b3

3. Расширение.

Для выделения некоторого числа новых факторов и построения необходимых для расчетов факторных показателей применяют прием расширения факторных моделей. При этом числитель и знаменатель умножаются на одно и тоже число.

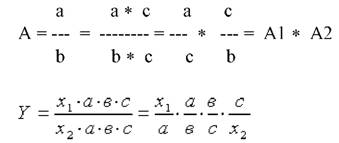
4. Сокращение.

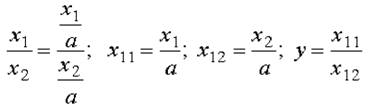
Для построения новых факторных показателей применяют прием сокращения факторных моделей. При использовании данного приема числитель и знаменатель делят на одно и то же число.

Процесс   моделирования   сложный   и   ответственный   момент. От реальности и точности моделей зависят конечные результаты анализа.

Детализация в факторном анализе во многом определяется числом факторов, влияние которых можно количественные оценить, поэтому большое значение в анализе имеют многофакторные мультипликативные модели.

В основе их построения лежат следующие принципы:

• место каждого фактора в модели должно соответствовать его роли в формировании результативного показателя;
• модель должна строиться из двухфакторной полной модели путем последовательного расчленения факторов, как правило качественных, на составляющие;
• при написании формулы многофакторной модели факторы должны располагаться слева направо в порядке их замены.

Построение факторной модели — первый этап детерминированного анализа. Далее определяют способ оценки влияния факторов.

Бальжинов А.В., Михеева Е.В. Анализ и диагностика финансово-хозяйственной деятельности предприятия: Учебн.пособ., — Улан-Удэ, 2003.

Поделиться
Добавить в закладки

Добавить комментарии

Методика расчета пофакторных влияний на прибыль

Методика расчета пофакторных влияний на прибыль от деятельности организации проходит несколько стадий.

Стадия 1. Расчет влияния фактора «выручка от продаж»

Рассчитаем влияние этого фактора в два приема. Выручка организации – количество, умноженное на цену продаваемой продукции. В первую очередь логично рассчитать влияние цены на прибыль от продаж. Во вторую очередь рассчитаем влияние изменение физической массы продукции на прибыль.

Пример 3

ОАО «Конус» имеет своей продукцией чугун и сталь. Учитываем инфляционное влияние – 14%. Учитываем повышение цен на собственную продукцию. В нашем случае используем только данные по инфляции.

Индекс ценn=100+14100=1,14.

Выручка от продаж в отчетном периоде составит

B’=B1Jп.

Где В′ — выручка от продаж в сопоставимых ценах, Вt, — выручка от продаж в отчетном периоде. ОАО имеет выручку в сопоставимых ценах:

В’=202 102 7311,14=177 283 097 тыс. руб.

Выручка увеличилась на 24,8 млрд. руб. Рост количества продаваемой продукции увеличил выручку в отчетном периоде на 24, 4 млрд. руб.

∆Bη=В1-В1Jп=В1-В’= 202 102 731-177 283 097==24 819 633 тыс. руб.;

∆Вкол=В’-В=177 283 097-154 880 576=22 402 521 тыс. руб.

Прирост за счет увеличения цены больше, чем за счет увеличения количества. Это говорит о росте качества продукции, положительный показатель для предприятия.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Стадия 2. Расчет влияния фактора «цена»

Определяем, как изменение цены влияет на прибыль от продаж.

∆Пп(к)=∆Вк·Rп100.

Где Rп – рентабельность продаж в основном периоде, то есть степень прибыли от продаж в процентах к выручке.

∆Пп(к)=∆Вк·Rп100=24 819 633·32100=7 942 283 тыс. руб.

Инфляционное влияние в сравнении с прошлым годом привело к росту прибыли от продаж, и сумма составила 7 942 283 тыс. руб.

Стадия 3. Расчет влияния фактора «количество проданной продукции»

Если количество продукции, которая продана меняется, это влияет на прибыль от продаж. Показатель рассчитывается так:

∆Пп(к)=((В1-В)-∆Вк)·Rп100=∆Вк·Rп100.

 Где ∆П – меняющаяся прибыль продаж;

В и В – выручка от продаж в двух периодах периодах;

∆Вк – изменение выручки, на которую повлияла цена;

Rп –  процентное соотношение уровня прибыли к выручке.

∆Пп(к)=((В1-В)-∆Вк)·Rп100=∆Вк·Rп100==22 402 521·32100=72 168 807 тыс. руб.

Наблюдается положительное влияние фактора, потому что рост объема выручки в отчетном периоде дал увеличение прибыли от продаж на 7 168 807 тыс. руб.

Стадия 4. Расчет влияния фактора «себестоимость проданной продукции»

∆Пп(с)=В1·УС1-УС100.

УС1 и УС – степень себестоимости в отчетном и базисном периодах

∆Пп(с)=В1·УС1-УС100==202 102 731·56,69-60,08100=-6 312 702 тыс. руб.

Нужно учесть, что расходы влияют на прибыль в обратном порядке. Наблюдается увеличение себестоимости на 22,1 млрд. руб. Но в соотношении с выручкой уровень продаж стал ниже на 3,13 %. Прибыль от продаж увеличилась на 6,3 млрд. руб. за счет экономии.

Стадия 5. Расчет влияния фактора «коммерческие расходы»

∆Пп(р)=В1·УКР1-УКР100.

УКР1 и УКР – степень расходов коммерческого направления в двух периодах.

∆Пп(р)=В1·УКР1-УКР100==202 102 731·5,37-5,89100=-1 058 047 тыс. руб.

Наблюдается увеличение прибыли от продаж на 1,06 млрд. руб., благодаря экономии коммерческих расходов и понижения их уровня по отношению к выручке.

Стадия 6. Расчет влияния фактора «управленческие расходы»

∆Пп(уур)=В1·УУР1-УУР100

УУР1, и УУР — степень управленческих расходов в двух периодах.

∆Пп(уур)=В1·УУР1-УУР100==202 102 731·1,83-1,9100=-136 699 тыс. руб.

Прибыль от продаж увеличилась на 136 699 тыс. руб. за счет снижения УР по отношению к выручке. Их уровень снизился на ,07%.

Факторный анализ прибыли и рентабельности организации позволил сделать вывод о том, что факторы хорошо влияют на прибыль.

Другие факторы не оказывают воздействия на прибыль от продаж так существенно, как хозяйственные. Представим обобщенную информацию факторного анализа рентабельности в таблице:

Мы видим, что факторы прибыль увеличивают. Рассмотрим коэффициент соотношения доходов и расходов:К=Все доходыВсерасходы. Если коэффициент больше единицы, деятельность организации можно считать эффективной. Для ОАО «Конус» это 1,256 в отчетном и 1,212 – в предыдущем периодах.

Формулы факторного анализа

Во всех современных статистических пакетах есть программы для корреляционного и факторного анализов. Компьютерная программа по факторному анализу по существу пытается «объяснить» корреляции между переменными в терминах небольшого числа факторов.

Факторы анализ проводится с использованием формул. Формулы варьируются в зависимости от модели. Так, аддитивные модели факторного анализа представляют собой алгебраическую сумму показателей и имеют вид:

Мультипликативные модели факторного анализ а в обобщенном виде могут быть представлены формулой:

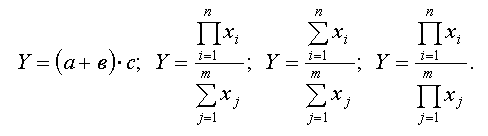
Кратные модели факторного анализа рассчитываются по формуле:

Смешанные модели представляют собой комбинацию перечисленных выше моделей и могут быть описаны с помощью специальных выражений:

Пример матрицы

Из матрицы видно, что корреляция между переменной V1 и первым фактором = 0,91. Чем выше факторная нагрузка, тем больше ее связь с фактором.

Существует одно принципиально важное свойство коэффициента корреляции, благодаря которому составляются описательные характеристики. Коэффициент корреляции, возведенный в квадрат, показывает, какая часть дисперсии (вариативности) признака является общей для двух переменных, или, говоря проще, насколько эти переменные перекрываются

Например, 2 переменные с корреляцией 0,9 перекрываются со степенью 0,9 * 0,9 = 0,81. Т.е. 81% дисперсии той и другой переменной являются общими, т.е. совпадают. Чтобы вычислить собственные значения фактора 1, нужно возвести в квадрат факторные нагрузки и сложить их по столбцу. 0,91*0,91 + 0,20*0,20 + 0,94*0,94 = 1,7517. Если собственное значение фактора разделить на число переменных, полученное число покажет, какая доля дисперсии объясняется данным фактором. 1,7517: 3 = 0,5839. Фактор 1 объясняет около 58 % информации.

КМО 0,9 и больше – безусловная адекватность, 0,8 – высокая применимость, 0,7 – приемлемая, 0,6 – удовлетворительная, 0,5 – низкая, Меньше 0,5 – факторный анализ не приемлем для данной выборки. Значение Bartletta должно быть не меньше 0,05.

Условия применения факторного анализа:

• нельзя факторизовать качественные данные, полученные по шкале наименований, например, цвет волос, глаз и т.д.
• все переменные должны быть независимым, а их распределение должно приближаться к нормальному.
• связи между переменными должны быть приблизительно линейны или не иметь явно криволинейного характера,
• в исходной корреляционной матрице должно быть несколько корреляций по модулю выше 0,3. Иначе – трудно извлечь из матрицы какие-либо факторы.
• выборка испытуемых должна быть достаточно большой (желательно 100 испытуемых).

Литература

1. Тугушев Р.Х. Особенности факторного анализа в психологии // Известия Саратовского университета. 2006. Т. 6. Сер. Философия. Психология. Педагогика, вып. 1/2
2. Ермолаев О.Ю. Математическая статистика для психологов – М.: Московский психолого-социальный институт, Флинта, 2003.

Понятие и задачи факторного анализа

Факторный анализ относится к статистическим методам психологии. Сущность метода состоит в наличии так называемого «фактора». Смысл фактора состоит в том, что им определяется некоторая ненаблюдаемая и прямо не измеряемая величина, категория, связанная с множеством близких к ней характеристик, которые могут быть измерены .

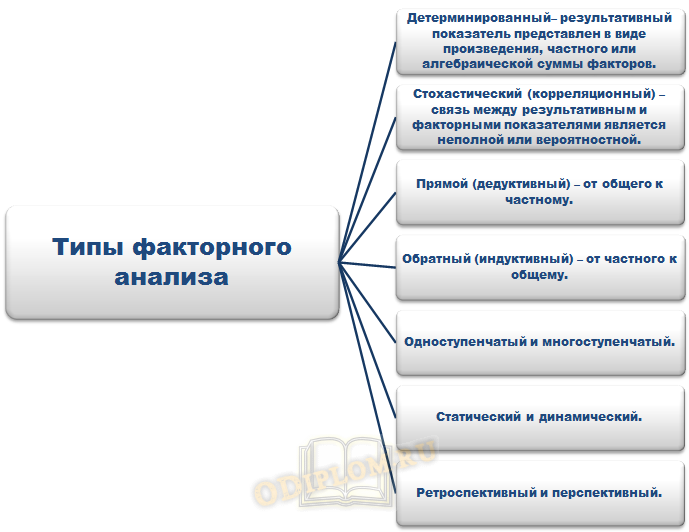
Типы факторного анализа

Факторный анализ в психологии призван использоваться при обработке больших массивов экспериментальных данных. В него входит комплекс аналитических методов, позволяющих выявить скрытые латентные признаки, а так же причины их возникновения и внутренние закономерности их взаимосвязи.

Факторный анализ – это раздел многомерного статистического анализа, объединяющий методы оценки размерности множества наблюдаемых переменных посредством исследования структуры ковариационных или корреляционных матриц .

Ключевые задачи факторного анализа представлены на рисунке ниже.

Задачи факторного анализа

Задачи факторного анализа определяют специфику его использования, а именно: факторный анализ используется как метод сокращения данных или как метод структурной классификации.

Важное отличие факторного анализа от всех других методов в том, что его нельзя применять для обработки первичных, или, как говорят, «сырых», экспериментальных данных, т.е. полученных непосредственно при обследовании испытуемых

Материалом для факторного анализа служат корреляционные связи, а точнее – коэффициенты корреляции Пирсона, которые вычисляются между переменными, включенными в обследование. Иными словами, факторному анализу подвергаются корреляционные матрицы.

Факторный анализ в Excel: пример

Факторным называют многомерный анализ взаимосвязей между значениями переменных. С помощью данного метода можно решить важнейшие задачи:

• всесторонне описать измеряемый объект (причем емко, компактно);
• выявить скрытые переменные значения, определяющие наличие линейных статистических корреляций;
• классифицировать переменные (определить взаимосвязи между ними);
• сократить число необходимых переменных.

Рассмотрим на примере проведение факторного анализа. Допустим, нам известны продажи каких-либо товаров за последние 4 месяца. Необходимо проанализировать, какие наименования пользуются спросом, а какие нет.

1. Посмотрим, за счет, каких наименований произошел основной рост по итогам второго месяца. Если продажи какого-то товара выросли, положительная дельта – в столбец «Рост». Отрицательная – «Снижение». Формула в Excel для «роста»: =ЕСЛИ((C2-B2)>0;C2-B2;0), где С2-В2 – разница между 2 и 1 месяцем. Формула для «снижения»: =ЕСЛИ(J3=0;B2-C2;0), где J3 – ссылка на ячейку слева («Рост»). Во втором столбце – сумма предыдущего значения и предыдущего роста за вычетом текущего снижения.
2. Рассчитаем процент роста по каждому наименованию товара. Формула: =ЕСЛИ(J3/$I$11=0;-K3/$I$11;J3/$I$11). Где J3/$I$11 – отношение «роста» к итогу за 2 месяц, ;-K3/$I$11 – отношение «снижения» к итогу за 2 месяц.
3. Выделяем область данных для построения диаграммы. Переходим на вкладку «Вставка» — «Гистограмма».
4. Поработаем с подписями и цветами. Уберем накопительный итог через «Формат ряда данных» — «Заливка» («Нет заливки»). С помощью данного инструментария меняем цвет для «снижения» и «роста».

Теперь наглядно видно, продажи какого товара дают основной рост.

Нахождение первичной структуры факторов

Метод главных компонент

Метод главных компонент стремится выделить оси, вдоль которых количество
информации максимально, и перейти к ним от исходной системы координат. При этом
некоторое количество информации может теряться, но зато сокращается размерность.

Этот метод проходит практически через весь факторный анализ, и может меняться
путем подачи на вход разных матриц, но суть его остается неизменной.

Основной математический метод получения главных осей — нахождение собственных
чисел и собственных векторов ковариационной матрицы таких, что:

RV = λV, где 

λ — собственное число R, R — матрица ковариации, V
— собственный вектор R. Тогда :

RV − λV = 0
V(R − λE) = 0 

и решение есть когда:

 | R − λE |  = 0, 

где R — матрица ковариации, λ — собственное число
R, E — единичная матрица. Затем считаем этот определитель для матрицы
соответствующей размерности.

V находим, подставляя собственные числа по очереди в

V(R − λE) = 0 

и решая соответствующие системы уравнений.

Сумма собственных чисел равна числу переменных, произведение — детерминанту
корелляционной матрицы. Собственное число представляет собой дисперсию оси,
наибольшее — первой и далее по убыванию до наименьшего — количество информации
вдоль последней оси. Доля дисперсии, приходящаяся на данную компоненту,
считается отсюда легко: надо разделить собственное число на число переменных m.

Коэффициенты нагрузок для главных компонент получаются делением коэффициентов
собственных векторов на квадратный корень соответствующих собственных чисел.

Алгоритм NIPALS вычисления главных
компонент

На практике чаще всего для определения главных компонент используют
итерационные методы, к примеру, NIPALS:

0. Задается 0 < ε₁ < 1 — критерий
окончания поиска главного компонента, и 0 < ε₂
< 1 — критерий окончания поиска главных компонентов, исходная
отцентрированная матрица X, i=1 — номер
главной компоненты.

1. Берется — вектор-столбец, k —
шаг алгоритма, j — любой столбец (просто чтобы было с чего начинать
апроксимизацию).

2. Вектор T_k
транспонируется.

3. Считается .

4. P_k нормируется

5. Считается новый

6. Если то и P_k — вектора весов и нагрузок
соответственно для i-ой главной компоненты. Если нет, то и
иди на 2.

7. .

8. Если | X | < ε, то стоп — найдены все
основные компоненты, нас удовлетворяющие. Иначе i++. Иди на 1.

Показатели рентабельности

Отражают продуктивность работы организации в общем контексте. Величина рентабельности – это эффективность и наличные или ресурсы, которые были использованы, в соотношении.

Рассчитаем показатели рентабельности для ОАО «Конус».

Пример 1

Рентабельность продаж:

Reпродаж=Прибыль от продажВыручка.

Re=49 759 429154 880 576=,32, т.е. 32% – за прошлый период;

Re1=72 438 229202 102 731=,36, т.е. 36% – за отчетный период.

Наблюдается увеличение в отчетном периоде на 4%. Прибыль составила ,36руб. с руб. продаж. Такая рентабельность является высокой для определенной отрасли, например, металлургии.

Чистая рентабельность:

Re=Чистая прибыльВыручка.

Re=40 423 931154 880 576=,26, т.е. 26% – за прошлый период;

Re1=71 675 882202 102 731=,35, т.е. 35% – за отчетный период.

Наблюдается увеличение чистой рентабельности на 9%.

Чтобы дать внешнюю оценку деятельности предприятия необходимо произвести анализ рентабельности активов и рентабельности собственного капитала.

Пример 2

Экономическая рентабельность или рентабельность активов:

Re=Чистая прибыльСредняя стоимость имущества·100%.

Re=40 423 931198779 196= 20% за прошедший период;

Re1=71 675 882276149 402= 26% за отчетный период.

Наблюдается прибыль организации в расчете на 1 руб. имущества в размере 6%.

Рентабельность собственного капитала:

Устанавливает соотношение величины инвестируемых собственных ресурсов и прибыли, полученной от их использования.

Re= Чистая прибыльСредняя стоимость собственного капитала· 100%.

Re =40 423 931170 502 329= 24% за прошедший период.Rе1=71 675 882207 074 247= 35% за отчетный период.

Наблюдается рост рентабельности собственного капитала на 11%, что означает увеличение размера прибыли на собственные основные средства, это положительно повлияет на развитие предприятия.

Проверка достоверности

Из многочисленных научных эссе известно, что для оценки достоверности данных учёные используют коэффициент Кронбаха. При этом под валидностью в исследованиях понимается близость измеренных значений.

При определении степени достоверности данных в исследовательской деятельности используются KMO (мера выборочной адекватности Кайзера-Мейера-Олкина) и тест сферичности Бартлетта. А для оценки надёжности и достоверности факторов применяют программное обеспечение SPSS, преимуществами которого являются наличие передовых инструментов статистического анализа, обширной библиотеки алгоритмов машинного обучения, анализа текста, расширений компонентов с открытым кодом, интеграции с большими данными и беспрепятственного внедрения в другие приложения.

При правильном подходе методы факторного анализа позволяют эффективно преодолеть проблемы, связанные с корреляцией причинных обстоятельств, и делать объективную оценку уровня экономического развития любой страны.